Modul pružnosti je jednou ze základních charakteristik betonu definujících jeho pružné deformace a hraje významnou roli při statickém návrhu konstrukcí. Vlivem současných trendů technologie betonu, nabízející širokou variabilitu návrhů složení betonů, dochází ke změnám nejenom pevnostních charakteristik, ale i modulů pružnosti betonu.
Modul pružnosti je základní charakteristikou betonu vypovídající o jeho přetvárných vlastnostech a ovlivňující deformační chování betonových konstrukcí. Je tak nezbytným parametrem pro správné statické modelování chování betonových konstrukcí.
V minulosti byly vytvořeny teoretické modely pro predikci vztahů mezi modulem pružnosti betonu a pevnostními charakteristikami betonů, které umožnily určit modul pružnosti výpočtem bez nutnosti jeho reálného měření. Nejčastěji je statický modul pružnosti vztahován k pevnosti v tlaku, ovšem jak vyplývá z teorií vnitřního systému chování betonu, kde se každý element (kamenivo, tranzitní zóna (interfacial transition zone – ITZ), cementová pasta) vyznačuje značnými rozdíly ve schopnosti přenášet napětí a rozdílným pevnostním chováním, nelze tyto teorie o současných betonech přejímat bez ověření reálných hodnot [1], [2].
Rychlý vývoj technologie betonu udává nové možnosti pro využití pevnostního potenciálu betonu. Dnes je možné bez značných potíží vyrobit betony s pevnostmi kolem 120 N/mm2 s použitím tradičních materiálů a současných metod návrhu složení betonu. Oproti pevnostem se modul pružnosti však zvyšuje v mnohem menší míře. Např. zatímco pevnost betonu je možné při použití shodných vstupních surovin (zejména typu a maximálního zrna kameniva a druhu cementu) zvýšit z 50 N/mm2 na 100 N/mm2, u modulu pružnosti je navýšení možné pouze o cca 20 %.
Charakteristické vlastnosti betonu
Vlastnosti zatvrdlých betonů lze rozdělit do čtyř skupin na základě jejich společných znaků [3]:
- mechanické – pevnost betonu v tlaku, příčném tahu, tahu za ohybu, prostém tahu a ve smyku,
- deformační – vlastnosti související se změnou objemu vlivem vnějších sil (modul pružnosti, dotvarování betonu) nebo vlivem vnitřních sil (smrštění, nabývání betonu),
- permeabilita – popisuje pohyb média nebo tok energie betonem (vzlínavost, nasákavost, vodotěsnost, elektrická vodivost aj.),
- trvanlivost – odolnost proti působení vnějších činitelů (ohnivzdornost, mrazuvzdornost, obrusnost) a odolnost proti působení chemických médií z ovzduší a kapalin.
Mechanické vlastnosti betonu udávají vztah mezi mechanickým namáháním a odporem, kterým materiál účinkům tohoto namáhání vzdoruje. Nejvýznamnějšími mechanickými vlastnostmi betonu je pevnost a odolnost proti přetvoření. V případě namáhání pouze mechanickým namáháním se mechanické vlastnosti materiálu označují jako vlastnosti přetvárné (deformační) nebo jako vlastnosti pevnostní, závislé na charakteru chování materiálu, který si buď zachovává svoji celistvost, nebo se nachází ve fázi porušování. Fyzikálně-mechanické vlastnosti betonu lze v zásadě modifikovat již ve fázi návrhu betonu výběrem vhodných surovin a jeho složením [4].
Deformační vlastnosti betonu – působením mechanického napětí dochází ve struktuře pevných látek ke změnám vzdálenosti mezi jednotlivými částicemi, k jejich vzájemným posunům i k složitým strukturálním změnám, v důsledku čehož mění tuhá tělesa do určité míry tvar i objem. Tyto změny jsou označovány jako přetvoření nebo také deformace. Pro statický výpočet konstrukcí jsou ukazateli přetvárnosti modul pružnosti a modul přetvárnosti. Přetvárnostní charakteristiky betonu se rozdělují následovně [5], [6]:
- statické – projeví se po krátkodobém nebo v krátké době několikrát opakovaném zatížení,
- dynamické – projeví se po mnohokrát opakovaném cyklickém zatížení,
- reologické – projeví se při dlouhodobém zatížení, označují se jako dotvarování.
Velikost deformace materiálu se vyjadřuje formou poměrného přetvoření, které představuje poměr změny rozměru k původnímu rozměru. Beton je materiál přenášející v konstrukci především tlaková napětí, proto je pružné chování nejdůležitější při jeho tlakovém namáhání, kdy dochází ke zmenšení rozměru ve směru působící síly [7]. Přetvoření nosných konstrukcí je charakterizováno velikostí a průběhem poměrných přetvoření materiálů v závislosti na velikosti napětí.
Každá konstrukce je zatěžována vnějším prostředím, které může vyvolat vratné či nevratné změny konstrukce. V případě změn hladiny statického napětí se jedná o změnu tvaru, tedy vyvolání deformací, přičemž je toto napětí měřitelné [8]. V případě betonu se setkáváme se dvěma druhy deformací. V první řadě se jedná o deformace vyvolané působením vnějšího zatížení (dotvarování) a v druhé řadě o deformace nezávislé na zatížení (smršťování, bobtnání, teplotní deformace aj.).
Pracovní diagram betonu
Tuhost betonu je nejlépe charakterizovaná pracovním diagramem při osovém namáhaní (tlak-tah). Diagramy mohou být zhotovené bez odlehčování nebo s odlehčováním. Podle typu diagramu jsou definované i deformační vlastnosti. Průběh přetvárnosti betonu při působení statického zatížení se liší v závislosti na jakosti betonu, tj. deformačních vlastnostech kameniva, množství, hutnosti, jakosti a stáří cementového kamene a rychlosti zatěžování, popř. na opakování zatížení.
Pracovní diagram definuje základní vlastnosti materiálu:
- deformační chování,
- mez kluzu – tzv. kritické napětí, při kterém materiál přechází ze stavu pružného do stavu tvárného, přičemž při tomto napětí vzrůstá deformace i bez nutnosti zvyšování napětí,
- mez pevnosti – nejvyšší dosažené napětí,
- houževnatost – měřítkem je množství přetvárné práce,
- modul pružnosti a přetvárnosti.
Tvar pracovního diagramu (obr. 1) závisí na rychlosti zatěžování a taktéž na zatěžovacím režimu.
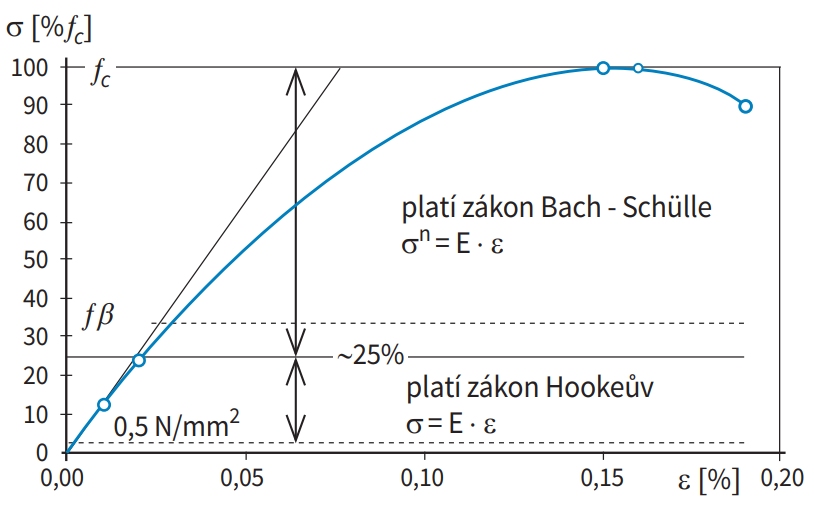
V oblasti pružných deformací platí Hookeův zákon. V oblasti deformací nepružných se stanovuje modul přetvárnosti vyjádřený poměrem napětí k celkovému poměrnému přetvoření. Skutečnost, že hmoty nejsou dokonale pružné a že ani pružná deformace není lineární, vedla k zavedení výrazu modul pružnosti podle Bach-Schüllea, jež je obdobou Hookeova zákona [6].
Modul pružnosti betonu
Modul pružnosti stanovuje závislost mezi napětím a přetvořením za definovaných podmínek měření změny napětí a změny přetvoření podle vztahu:
E = σ / ε (1)
kde E je modul pružnosti [MPa], σ napětí [MPa] a ε poměrné přetvoření.
Moduly pružnosti je možné rozdělit na:
- statický modul pružnosti stanovený ze závislosti mezi napětím a poměrným přetvořením,
- sečnový modul pružnosti, který je daný poměrem σx/εx,
- tečnový modul pružnosti daný směrnicí ke křivce mezi napětím a deformací při daném napětí,
- začáteční tečnový modul pružnosti, který je směrnicí ke křivce v začátku závislosti (obr. 2) a dosahuje nejvyšší hodnoty. Tečnový modul pružnosti je naopak nejnižší a sečnový modul má hodnotu mezi nimi [9].
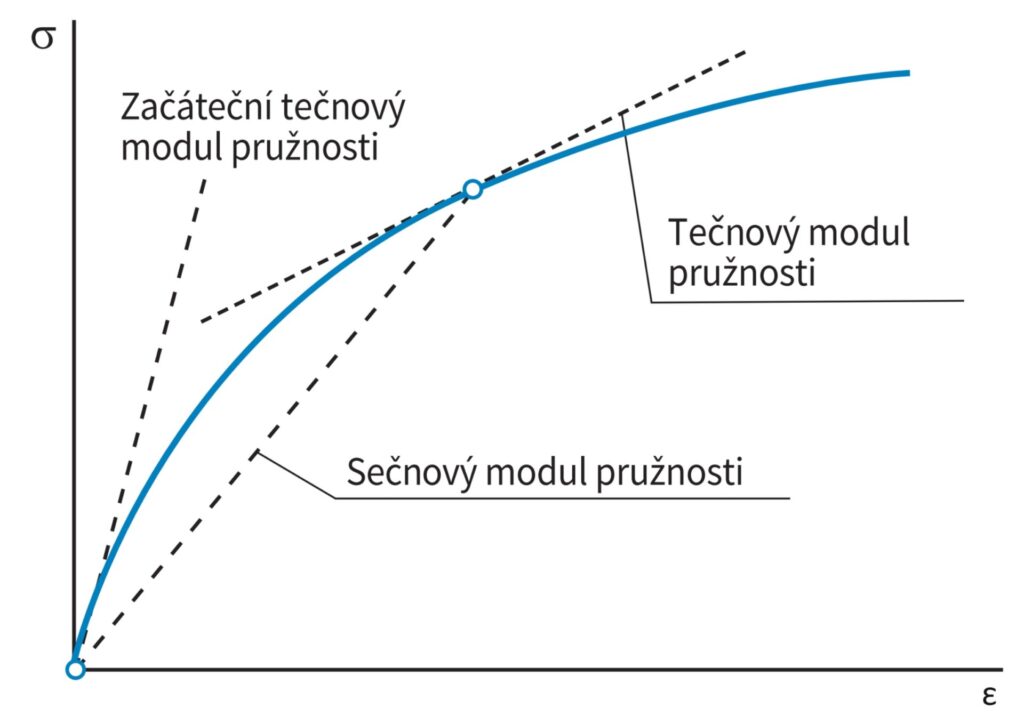
Jelikož je beton nelineárně pružný materiál, s narůstajícím napětím se výrazně zvyšuje jeho deformace. S narůstajícím napětím se tedy zmenšuje strmost sečny, což znamená, že čím vyšší je napětí při stanovení modulu pružnosti, tím nižší je jeho hodnota.
Faktory ovlivňující modul pružnosti betonu
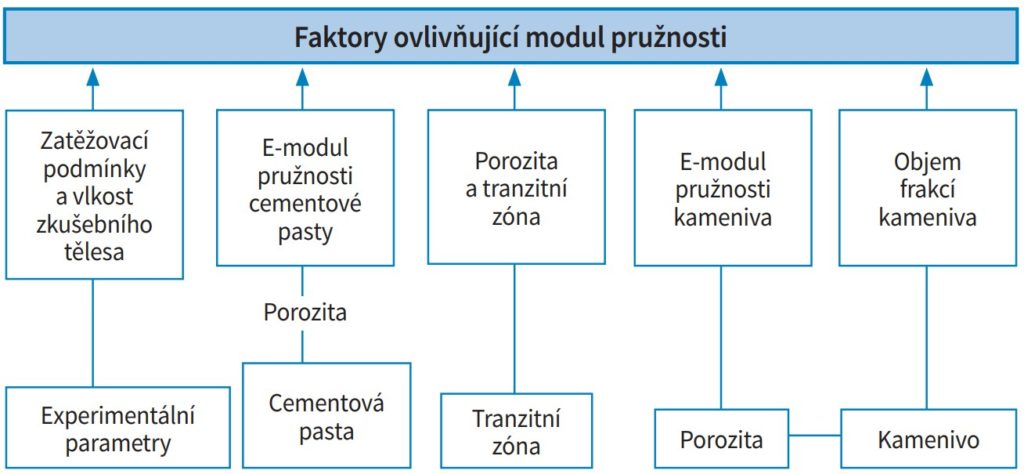
Na výslednou hodnotu modulu pružnosti betonu má vliv celá škála různých faktorů, které jsou popisovány v odborné literatuře. Základní faktory se dělí do dvou skupin [10]:
- technologické – složení betonu (typ cementů a příměsí, druh kameniva, granulometrie a maximální zrno kameniva, typ a dávka plastifikačních přísad, vodní součinitel, provzdušnění betonu, tloušťka a kvalita tranzitní zóny – ITZ), ukládání, zhutňování a ošetřování betonu,
- zkušební – tvar a velikost zkušebního tělesa (válce, trámce), stáří zkušebního tělesa, rychlost zatěžování, excentricita apod.
Technologické faktory
V případě vlivu kameniva a cementové pasty je možné sledovat prakticky lineární závislost mezi napětím a poměrným přetvořením, ovšem v případě betonu jako kompozitního materiálu je tato závislost nelineární. Příčinou nelinearity je existence vzájemných vazeb mezi povrchem kameniva a cementovou pastou (kvalita, tloušťka tranzitní zóny), rozvoj mikrotrhlin a vznik lokálních napětí v této oblasti [7].
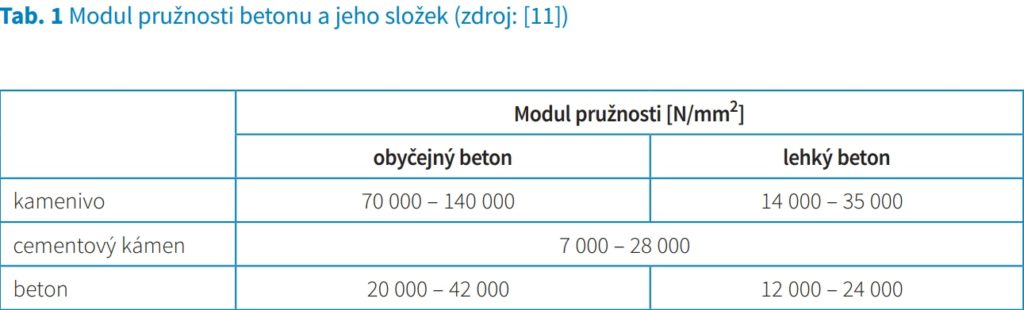
Modul pružnosti betonu je podstatně odlišný od modulu pružnosti ztvrdlé cementové pasty [11], což ukazuje na rozdílnost modulů pružnosti složek betonu, přičemž kamenivo má jednoznačně vyšší modul pružnosti než zhydratovaná cementová pasta a vyšší obsah kvalitního hrubého kameniva tak přináší vyšší modul pružnosti betonu. Mechanické vlastnosti cementového kamene závisí, při stejných podmínkách zatížení a vnějšího prostředí, na množství, druhu, rozměru a orientaci pórů a trhlinek. Ztvrdlý cement a kamenivo ovlivňují velkým podílem přetvárné vlastnosti (deformace). Je-li podíl cementu v betonu okolo 15 %, existuje vysoký potenciál na výrazné ovlivnění deformačních vlastností betonu. Jak je patrné z obr. 3, čím vyšší bude obsah kameniva, tím blíže bude křivka betonu ke křivce kameniva. Naopak v betonu s vyšší dávkou cementu bude křivka blíže ke křivce cementové pasty.
Modul pružnosti betonu se tak pohybuje mezi modulem pružnosti cementové pasty a modulem pružnosti kameniva.
Výrazný vliv na modul pružnosti cementového kamene má jeho pórovitost, kdy se zvyšující se pórovitostí betonu dochází ke snížení výsledné hodnoty modulu pružnosti betonu. Pórovitost cementové pasty při zvyšujícím se vodním součiniteli w/c navyšuje obsah volné vody v čerstvém betonu. Kapilární pórovitost podstatně ovlivňuje pevnost betonu v tlaku a ve své podstatě shodně i modul pružnosti. Modul pružnosti je přibližně úměrný třetí mocnině poměru gel/prostor. Při uvažování kapilární pórovitosti cementové kaše se uplatňuje následující vztah:
Ep = Eg (1 — Pc)k, (2)
kde Ep je modul pružnosti ztvrdlé cementové kaše, Eg modul pružnosti ztvrdlé cementové kaše při nulové pórovitosti, Pc kapilární pórovitost a k konstanta udávající hodnotu v závislosti na modulu pružnosti ztvrdlé cementové pasty (Eg = 72 500 N/mm2, když k = 3, a Eg = 85 000 N/mm2, když k = 4) [3], [9].
Modul pružnosti roste se stářím cementového kamene a při uložení ve vodním prostředí je o 10 až 20 % vyšší oproti uložení na vzduchu do stáří cca 120 dnů [3].
Kamenivo
Modul pružnosti kameniva má vzhledem k jeho objemu v betonu výrazný vliv na modul pružnosti samotného betonu. Moduly pružnosti kameniva ovlivňuje mineralogické složení, textura a struktura hornin, ze kterých bylo kamenivo vyrobeno, a jsou velmi závislé na pórovitosti horniny.
Vlastnosti a objem zejména hrubého kameniva ovlivňují jak pevnost betonu v tlaku, tak modul pružnosti betonu, přičemž jejich vliv na modul pružnosti je vyšší než na pevnost v tlaku. Z tohoto důvodu bude mít beton vyrobený z méně pevného kameniva nižší modul pružnosti než beton se stejnou pevností vyrobený z pevnějšího kameniva. Nejen rozdílný druh kameniva, ale také stejný druh, ale z rozdílných lokalit může značně ovlivnit modul pružnosti betonu. Významnou roli má i stoupající velikost Dmax.
Zkušební faktory
Oproti technologickým faktorům, které jsou v podstatě ovlivněny samotným složením a výrobou betonu, jsou ty zkušební více či méně ovlivněny zkušebním zařízením, obsluhou strojů, zkušebním postupem a volbou úpravy zkušebních těles, jež jsou závislé především na možnostech laboratoře a místních zvyklostech. Nejčastější zkušební vlivy jsou následující:
- zkušební metoda,
- výpočetní vztah zatěžovací úrovně,
- tvar a velikost zkušebního tělesa (válce, trámce),
- způsob získání zkušebního tělesa,
- stáří zkušebního tělesa,
- použitý snímač,
- vliv zkušebního lisu,
- rychlost zatěžování,
- způsob zakoncování tlačných ploch zkušebního tělesa aj.
Technologické zásady pro zvýšení hodnot modulů pružnosti
S rychlým vývojem technologie betonu a s použitím nynějších dostupných materiálů a výrobních procesů dochází k nástupu betonů lišících se od základního konceptu cement → kamenivo → voda na cement → kamenivo → voda → přísady (plastifikační/superplastifikační), resp. cement → příměs → kamenivo → voda → přísady.
Kvůli intenzitě používání těchto složek pro výrobu betonu dochází ke značným změnám v poměrech mezi přetvárnými vlastnostmi a pevností betonu v tlaku [2], [12], a proto je nutné zásadně přehodnotit některé závislosti, ze kterých se následně vychází při statickém navrhování betonových konstrukcí. V dřívějších dobách byla postačující základní charakteristikou betonu jeho pevnost v tlaku, z níž se empiricky odvozovaly ostatní výpočtové charakteristiky jako např. pevnost v tahu za ohybu, příčný tah a statický modul pružnosti. Vlivem změn a trendů v oblasti navrhování a provádění betonových konstrukcí je však potřeba předvídat i další vlastnosti, jako jsou modul pružnosti, smrštění, dotvarování, propustnost a trvanlivost [13].
Empirický vztah mezi modulem pružnosti a pevností v tlaku může platit pouze pro betony s podobným složením, zejména pak u tradičních vibrovaných betonů. V případě větších rozdílů ve složení, v použitém kamenivu, druhu a dávce cementu, přísadách či příměsích může být tato závislost podstatně odlišná. To se týká zejména lehce zhutnitelných betonů s konzistencí nad S3 a dále betonů, při jejichž výrobě bylo použito směsných cementů, zejména vápencových, s narůstajícím objemem aktivních příměsí (elektrárenské popílky, mikromleté vápence, jemně mletá granulovaná vysokopecní struska) či některých typů superplastifikátorů.
Závěrečná doporučení
Pro dosažení relativně vyšších hodnot statických modulů pružnosti doporučujeme [2]:
- používat pouze portlandské cementy CEM I, v případě použití směsných cementů stejné pevnostní třídy lze očekávat snížení hodnot modulů pružnosti o cca 10 až 15 %. Totéž platí v případě použití kombinace cementů CEM I s aktivními příměsmi, např. elektrárenskými popílky či jemně mletou vysokopecní struskou. Aplikovat zažité zkušenosti s odhadem k-hodnoty a dopady na pevnosti v tlaku pro odhady statických modulů pružnosti je nebezpečné. Výsledné hodnoty modulů pružnosti budou nižší než pro stejnou pevnostní třídu vyrobenou pouze z cementu CEM I, omezit množství frakce 0 – 4 mm a jemných podílů pod 0,125 mm. Pokud to umožní reologické vlastnosti čerstvých betonů (čerpatelnost, zhutnitelnost), je lepší používat pro výpočet poměrů mísení směsi kameniva z více frakcí rovnice EMPA I, II než Fullerovu rovnici,
- využívat kameniva do maximální frakce 22 mm, přičemž lepší jsou drcená než těžená [12],
- využívat hrubá kameniva, která mají vysoký modul pružnosti, např. žula, čedič, diabas, amfibolit. Naopak usazeniny a některé přeměněné horniny mají modul pružnosti podstatně nižší. Mezi pevností v tlaku a modulem pružnosti neplatí vždy jednoznačná závislost. Např. diorit a gabro mají přibližně shodný modul pružnosti od 70 do 85 GPa, avšak jejich pevnosti jsou značné odlišné, a to 170 až 300 MPa,
- ověřit dopad typu a dávky superplastifikační přísady. Praxe ukazuje, že některé typy moduly pružnosti snižují. Ovšem je třeba mít na paměti, že čím je vodní součinitel nižší, tím je cementový kámen hutnější a tranzitní zóna (ITZ) kvalitnější, což moduly pružnosti ovlivňuje pozitivně,
- nečekat vysoké moduly u provzdušněných betonů,
- využívat možností dosažení požadovaných hodnot ve stáří 60 či 90 dnů. Dají se očekávat cca 6 – 10% nárůsty hodnot oproti hodnotám dosaženým ve stáří 28 dnů,
- v případě požadavku projektanta na konkrétní hodnoty statických modulů je třeba si ujasnit, zda se jedná o hodnotu minimální, průměrnou či maximální. Vzhledem k tomu, že nejsou stanovena hodnoticí kritéria pro soubory zkoušek, je nutné si před začátkem betonáží vyjasnit specifikaci betonu včetně postupu při neshodě výsledků, příp. jakým způsobem budou prováděny zkoušky na hotových konstrukcích,
- při požadavku na konkrétní hodnoty statických modulů pružnosti nad hodnoty 28 GPa provést průkazní zkoušky,
- nevycházet ze vztahů pro převod EC2 pouze z pevnostní třídy betonu. Je nutné reflektovat v současnosti stále více využívané vstupní suroviny jako směsné cementy, minerální příměsi a vysoce účinné plastifikační přísady pro výrobu betonu.
Článek vznikl za podpory projektu FV30325 Aplikace laserových a radarových měření vozovek do diagnostiky cementobetonových krytů dálnic, uplatnění mikroskopických a chemických analýz betonů pro omezení degradačních procesů betonů snižujících dobu životnosti dálničních vozovek.
Literatura
[1] AÏCTIN, P. C. Vysokohodnotný beton. Praha: Informační centrum ČKAIT, 2005. 320 s. ISBN 80 – 86769 – 39 – 9.
[2] KŘÍŽOVÁ, K. Studium závislostí složení betonů na hodnoty modulů pružnosti. Brno, 2013. Disertační práce. Vysoké učení technické v Brně, Fakulta stavební. 154 s.
[3] PYTLÍK, P. Technologie betonu. Brno: Akademické nakladatelství CERM, 1994. 143 s. ISBN 80 – 85867 – 07 – 9.
[4] ŠMERDA, Z. et al. Životnost betonových staveb. Praha: Český svaz stavebních inženýrů, 1999. 184 p. ISBN 80 – 902697‑8 – 8.
[5] NOVÁK, J. a kol. Nauka o materiálech 10: Stavební materiály I. Praha: ČVUT, 1997. 178 s. ISBN 80 – 01 – 01619 – 6.
[6] PAVLÍK, A., DOLEŽEL, J.,FIEDLER, K. Technologie betonu. Praha: Státní nakladatelství technické literatury, 1973. 322 s.
[7] UNČÍK, S., ŠEVČÍK, P. Modul pružnosti betonu. Trnava: Betón Racio, s. r. o., 2008. 24 s. ISBN 978 – 80 – 959182 – 3‑2.
[8] SCHMID, P. a kol. Základy zkušebnictví. Brno: Akademické nakladatelství CERM, s. r. o., 2000. 112 s. ISBN 80 – 214‑1816 – 8.
[9] BAJZA, A., ROUSEKOVÁ, I. Technológia betónu. Bratislava: Jaga Group, s. r. o., 2006. 190 s. ISBN 80 – 8076 – 032 – 2.
[10] HUŇKA, P., KOLÍSKO, J. Studium vlivu tvaru, velikosti a způsobu přípravy zkušebního tělesa na výsledek zkoušky statického modulu pružnosti betonu v tlaku. Beton TKS. 2011, roč. 11, č. 1, s. 69 – 71. ISSN 1213 – 3116.
[11] TOPCU, B., UGURLU, A. Elasticity Theory of Concrete and Prediction of Static E‑Modulus for Dam Concrete Using Composite [online]. 2007. Dostupný z: http://www.docstoc.com/docs/2220202/Elasticity-Theory-of-Concrete-and-Prediction-of-Static-E-Modulus
[12] RIEGER, P., ŠTĚRBA, A. Znovu k údajným problémům s modulem pružnosti betonu, možnost specifikace dle změny Z3 ČSN EN 206 – 1. Beton TKS. 2009, roč. 9, č. 4, s. 88 – 91. ISSN 1213 – 3116.
[13] NASSIF, H. H., NAJM, H., SUKSAWANG, N. Effect of puzzolanic materials and curing methods on the elastic modulus of HPC. Cement and Concrete Composities [online]. 2005, Vol. 27, Issue 6, p. 661 – 670. [cit. 2011-04-15]. Elsevier.


