V současné době není vláknobeton vyztužený ocelovými drátky zahrnut v aktuálně platném znění Eurokódu 2 [1]. Existuje však několik standardů a doporučení pro navrhování a posouzení konstrukcí z tohoto materiálu, z nichž nejrozšířenějším je německá směrnice DAfStb [2]. Firma Bekaert spolupracovala na vývoji řešení pro návrh a posouzení drátkobetonových konstrukcí s firmou Scia. Výsledkem je implementace nového modulu založeného na německé směrnici DAfStb do výpočetního prostředí programu Scia Engineer. Výsledky numerických simulací jsou porovnány s velkoformátovými experimenty základové desky na pilotách provedené pro tzv. Nanhui projekt na univerzitě v Šanghaji, kde byly porovnávány hodnoty mezních zatížení a směr šíření trhlin.
Rozvoj nových materiálů s sebou přináší nové požadavky na jejich navrhování. To platí i v případě betonových konstrukcí vyztužených ocelovými vlákny (SFRC – steel-fibre-reinforced concrete). V případě přidání ocelových vláken do betonové směsi dochází k výraznému zvýšení tahové pevnosti a větší tažnosti výsledného kompozitního materiálu. Hlavní otázkou pak zůstává, jakým způsobem efektivně verifikovat konstrukci z tohoto materiálu. V aktuální verzi Eurokódu 2 [1] pro budovy není o vláknobetonu žádná zmínka. Existují však jiné publikace a doporučení jako RILEM [3], Model Code 2010 [4] z roku 2014 a především německá směrnice DAfStb [2], která byla základem pro implementaci numerické analýzy v tomto článku. Tato směrnice rozšiřuje platnou německou národní přílohu DIN EN 1992 – 1‑1/NA. V současné době je v běhu také příprava nového vydání Eurokódu 2, kde je v pracovní verzi již obsažena kapitola L týkající se právě navrhování drátkobetonových konstrukcí. V mnohém se tato pasáž podobá právě německé směrnici DAfStb.
Vzhledem k nedostatku dostupných nástrojů pro každodenní navrhování těchto typů konstrukcí přináší firma Scia, jakožto vývojář programu Scia Engineer pro konečně prvkovou analýzu stavebních konstrukcí, první komplexní řešení, jež je výsledkem spolupráce se společností Bekaert, výrobcem ocelových drátků Dramix. Dostupné řešení integrované do programu Scia Engineer v sobě kombinuje:
- materiálovou databázi předdefinovaných vláken Dramix a
- výpočetní nástroj pro návrh a posouzení drátkobetonových konstrukcí podle DAfStb [2].
Návrhový přístup pro analýzu drátkobetonových konstrukcí podle DAfStb [2] je popsán v následujících kapitolách tohoto článku.
Drátkobetonové konstrukce v programu Scia Engineer
Společnost Scia spolu se společností Bekaert vyvinula unikátní řešení pro návrh a posouzení drátkobetonových plošných konstrukcí. Jedná se o první známou implementaci do počítačového programu (v tomto případě Scia Engineer) fungujícího na základě metody konečných prvků (MKP). Společnost Bekaert poskytla své znalosti a zkušenosti při vývoji a výrobě ocelových drátků. V programu je nově zakomponována speciální materiálová knihovna s předdefinovanými třídami betonu spolu se čtyřmi základními typy ocelových vláken Dramix: 5D 65/60BG, 5D 65/60GG, 4D 65/60BG a 3D 45/50BL [5].
Ověření konstrukcí je prováděno na základě posouzení pro mezní stav únosnosti (MSÚ):
- posouzení únosnosti (normálová síla a ohybový moment),
- posouzení smyku
a posouzení pro mezní stav použitelnosti (MSP):
- posouzení šířky trhlin,
- posouzení omezení napětí.
Navíc je možné provádět ověření lokálních oblastí v protlačení při kontaktu deska-sloup. Všechna posouzení mohou být spuštěna na předem stanovené množství vláken, příp. optimalizované množství na MSÚ.
Materiálové charakteristiky
Charakteristická tahová pevnost materiálu
Výpočet materiálových charakteristik je obecně závislý na typu a množství vláken, nejinak je tomu podle DAfStb [2]. Střední hodnoty reziduální tahové pevnosti fR1,m a fR4,m jsou základem pro stanovení pracovních diagramů (σ — ε). Tyto hodnoty jsou zjištěny na základě testů trámců ze SFRC a jsou ovlivněny množstvím a typem vláken a také třídou betonu. Charakteristické reziduální ohybové pevnosti (f fcflk,L1 a f fcflk,L2) jsou odvozeny ze středních hodnot ( fR1,m a fR4,m ). Protože jsou tyto střední hodnoty založeny na velkém množství provedených testů, je možné předpokládat, že prahová hodnota (0,51.fR) je dosažena pro všechny testované případy dle vzorce O.3 z DAfStb [2]. Výpočet charakteristických reziduálních tahových pevností (f fct0,L1; f fct0,L2; f fct0,u; f fct0,s) je dalším krokem v procesu výpočtu materiálových hodnot, kdy jsou charakteristické reziduální ohybové pevnosti převedeny na tahové pomocí součinitele β. Stanovení parametrů β je provedeno na základě obrázků P.1 a P.2 z DAfStb [2]:


Charakteristické reziduální tahové pevnosti jsou součástí materiálové databáze jako funkce typu a množství vláken spolu s třídou betonu.
Charakteristická tahová pevnost elementu
Dalším krokem stanovení materiálových charakteristik je výpočet reziduálních hodnot z charakteristických tahových pevností se zahrnutím vlivu velikosti prvku a orientace vláken. Předpokladem je uvažování velkých horizontálně litých desek, pro něž platí následující hodnoty:
- KfG = 1,7; vliv velikosti prvku; předdefinovaná jedna hodnota pro materiál a desku,
- KfG = vliv orientace vláken v kompozitu (1,0 pro tah a ohyb; 0,5 pro smyk):

Návrhové tahové pevnosti
Posledním krokem výpočtu materiálových charakteristik je stanovení návrhových z reziduálních charakteristických tahových hodnot na základě redukčních faktorů zohledňujících dlouhodobé působení (αfc = 0,85) a dílčích součinitelů spolehlivosti (γfct = 1,25) podle tabulky R.1 z [2]:
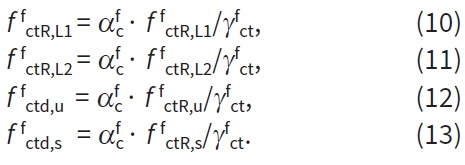
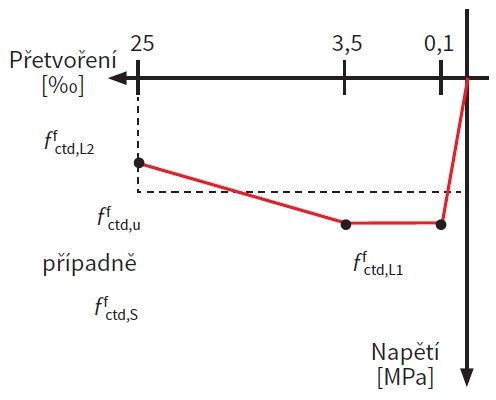
Tahové větve pracovních diagramů
Pracovní diagramy v tahu pro vláknobeton jsou odlišné od pracovních diagramů pro standardní železobeton. Vliv vláken je zohledněn uvažováním tahové větve materiálu. Obecně norma DAfSTb předepisuje dva typy pracovního diagramu vláknobetonu v tahu v závislosti na použitém typu analýzy.
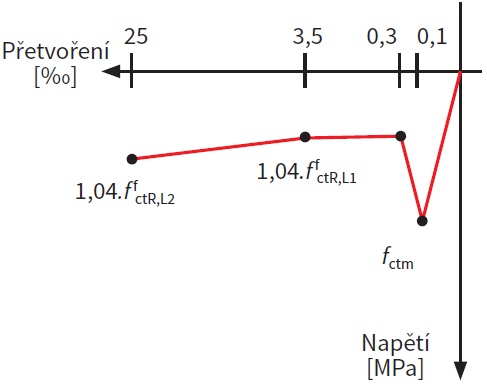
Návrh optimálního množství vláken a posouzení na kombinaci moment a normálová síla (MSÚ)
Stanovení optimálního množství vláken je založeno na iterativním výpočtu únosnosti průřezu v MSÚ zatíženého kombinací ohybového momentu a normálové síly. Logika na pozadí je vyvinuta tak, že se hledá optimální množství vláken v každém konečném prvku konstrukce, aby byla dosažena rovnováha na průřezu a maximální využití blízké 100 % v MSÚ. Navíc je také zahrnut vliv standardní betonářské výztuže, která se podílí na zvětšení únosnosti průřezu. Díky použití ocelových vláken je možné uvažovat také tahovou větev pracovního diagramu, což se jeví jako hlavní výhoda vláknobetonu. Pro výpočet v MSÚ je možné stanovit následující předpoklady:
- vláknobeton působí v tlaku i tahu,
- rovina přetvoření zůstává rovinná po aplikaci zatížení,
- platí rovnováha ohybových momentů a normálových sil v průřezu,
- maximální tlakové přetvoření betonu závisí na jeho třídě,
- pracovní diagram v tahu je na následujícím obr. a maximální tahové přetvoření je stanoveno na 25 ‰.
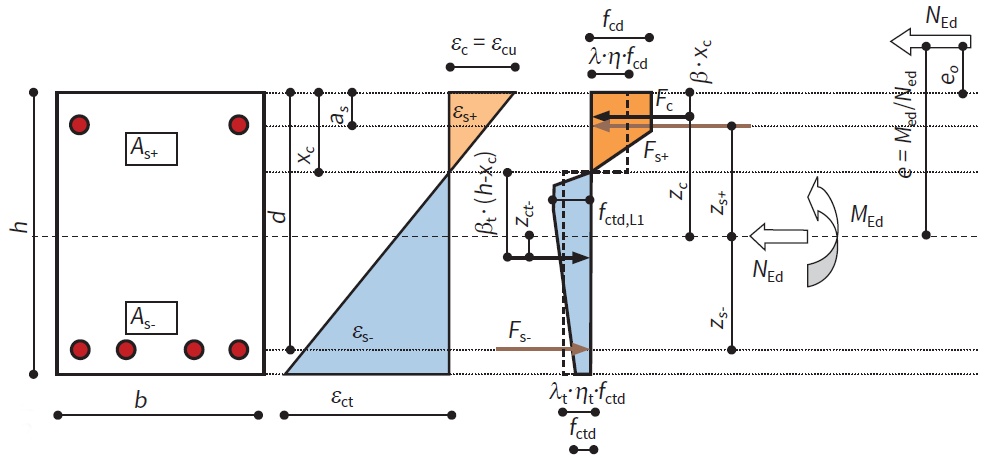
Rovnice pro stanovení rovnováhy normálových sil a ohybových momentů na průřezu je vyjádřena následovně:
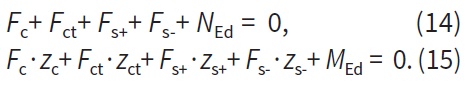
Smyková únosnost a protlačení
V případě průřezu s ocelovými vlákny je celková smyková únosnost (vfRd,c) uvažována jako součet běžné únosnosti ve smyku (vRd,c dle [1] a příspěvku ocelových vláken (vRd,cf). Tato vlákna se chovají jako rozptýlená výztuž a podílí se na přenosu smykového namáhání, což může vést k výraznému zvýšení smykové únosnosti a naopak ke snížení množství tradiční konvenční výztuže či v některých případech k jejímu kompletnímu vynechání:

Smyková únosnost je vypočtena podle kapitoly 6.2 normy [1]. Přírůstek smykové únosnosti vlivem vláken je vyjádřen pomocí článku 6.2.2 z [2] a je závislý na materiálových charakteristikách vláknobetonu, což lze vyjádřit následovně:
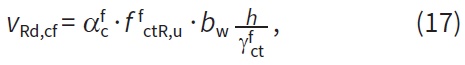
kde f fctR,u je charakteristická reziduální pevnost vláknobetonu v MSÚ.
Pro případ, že by byl vliv ocelových vláken na smykovou únosnost průřezu velmi významný, je na stranu bezpečnou omezena celková smyková únosnost vláknobetonu 140 % běžné smykové únosnosti železobetonového průřezu:
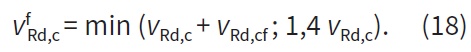
Příspěvek ocelových vláken na smykovou únosnost v protlačení je uvažován stejným způsobem. Nicméně v případě návrhu přídavné konvenční betonářské výztuže na protlačení nelze uvažovat vliv ocelových vláken na celkovou smykovou únosnost průřezu na základě Re 6.4.5 [2] a je nutné počítat pouze s betonem bez vláken.
Šířka trhliny a omezení napětí
Výpočet šířky trhliny koresponduje se základními předpoklady z EN1992‑1 – 1 pro tradiční konvenční výztuž [1]. Vliv ocelových vláken je uvažován přídavným redukčním faktorem αf, který reprezentuje poměr mezi charakteristickou reziduální pevností betonu v MSP (f fctR,s) a střední tahovou pevností betonu (fctm):
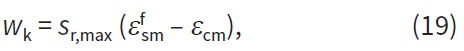
kde je maximální vzdálenost trhlin sr,max spočtena podle následujícího vztahu:
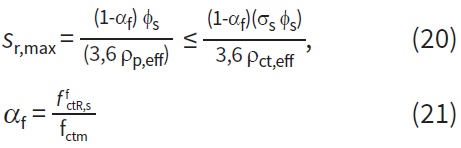
a rozdíl středních přetvoření ve výztuži a betonu (εfsm – εcm):
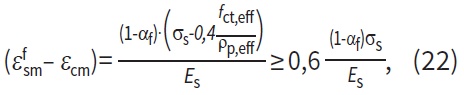
kde εfsm je střední přetvoření ve výztuži, εcm střední přetvoření v betonu mezi trhlinami, αf poměr charakteristické reziduální pevnosti vláknobetonu v MSP (ffctR,s) a střední tahové pevnosti betonu (fctm), øs průměr betonářské výztuže, ρp,eff efektivní poměr výztuže, fct,eff efektivní tahová pevnost betonu, Es modul pružnosti výztuže a σs napětí ve výztuži.

V případě vláknobetonu bez konvenční výztuže nelze využít vztah výše uvedený a je použitý odlišný zjednodušený přístup pro výpočet šířky trhliny založený na následujícím vzorci podle [2]:
kde sfw je konstantní délka 140 mm a εfct tahové přetvoření vláknobetonu.
Dalším signifikátorem pro ověření průřezu v MSP je posouzení omezení napětí v betonu a výztuži.
Pokud nevyhoví posudek na šířku trhliny, zpravidla nejsou splněny ani podmínky pro omezení napětí. Předpoklady výpočtu jsou stejné jako pro výpočet šířky trhliny a jsou kontrolovány následující stavy pro dílčí komponenty v průřezu:
- napětí v betonu pro charakteristickou kombinaci zatížení dle 7.2.(2) [1],
- napětí v betonu pro kvazistálou kombinaci zatížení dle 7.2.(3) [1],
- napětí v konvenční výztuži pro charakteristickou kombinaci zatížení dle 7.2.(5) [1].
Napětí v konvenční výztuži (σs) je počítáno bez vlivu ocelových vláken, což vede k mírně fiktivním hodnotám, kdy mohou být napětí ve výztuži vyšší než skutečné meze kluzu výztuže. Proto je zavedeno tzv. efektivní napětí ve výztuži ( σseff) zohledňující vliv ocelových vláken, které je porovnáváno s maximálním dovoleným napětím ve výztuži. Toto efektivní napětí se určí dle níže uvedeného vztahu dle [2]:

Srovnávací příklad
Na následujícím jednoduchém příkladu metrového výseku desky tloušťky 200 mm z betonu C25/30 bylo provedeno porovnání vypočtených hodnot pro vláknobeton s konvenční výztuží a železobeton vyztužený klasickou betonářskou výztuží. Použita jsou vlákna Dramix 4D 65/60BG o dávce 30 kg/m3. Přepočtené pevnostní charakteristiky vláknobetonu jsou f fctR,L1 = 1,25 MPa; f fctR,L2 = 1,44 MPa; f fctR,S = 1,15 MPa. V průřezu je použita betonářská výztuž B500B o průměru 10 mm po vzdálenosti 200 mm u spodního povrchu s krytím 30 mm.
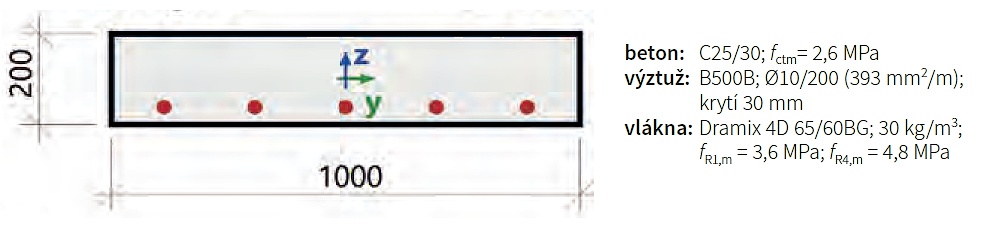
Pokud porovnáme únosnosti pro první mezí stav, dostaneme hodnoty MRCed = 30,3 kNm/m a MSFRCEd = 43,3 kNm/m. Jen pro porovnání, v případě čistého vláknobetonu bez konvenční výztuže bychom dostali MFCed = 17,6 kNm/m. Z vypočtených hodnot únosností je patrné, že díky reziduální tahové pevnosti má průřez z vláknobetonu o 43 % vyšší únosnost v ohybu než průřez s běžnou výztuží se stejným procentem vyztužení.
Pokud se zaměříme na únosnost ve smyku, dostáváme smykovou únosnost železobetonu vRCRd,c = 87,6 kN/m. Vliv vláken na únosnost ve smyku lze vyjádřit jako vRd,cf = 93,8 kN/m dle vzorce (17), což dává výslednou smykovou únosnost vláknobetonu dle vzorce (16) rovnu vfRd,c = 122,64 kN/m. Tato hodnota reprezentuje nárůst únosnosti ve smyku o 40 %. Prostý součet by dal ještě větší únosnost, ale zde se uplatní právě omezení na maximálně 140 % vRd,c, vztah (18).
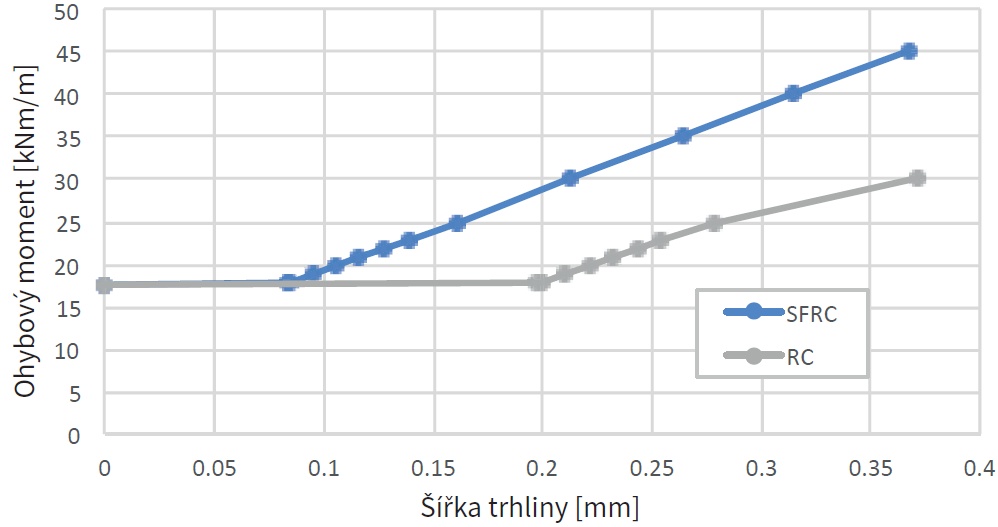
Na následujícím grafu je vyjádřen vztah mezi šířkou trhliny a působícím ohybovým momentem v MSP. Moment na mezi vzniku trhliny je pro oba materiály stejný MEd,SLS = 17,8 kNm/m. Pro tento ohybový moment dostáváme v případě vláknobetonu šířku trhliny wkSFRC = 0,083 mm při střední vzdálenosti mezi trhlinami sSFRCr,max = 172,3 mm, zatímco u železobetonu wkRC = 0,197 mm a sRCr,max= 225,8 mm, což je zhruba 2,3× vyšší hodnota šířky trhliny. Běžně používaná maximální šířka trhliny 0,3 mm je v případě vláknobetonu dosažena pro MSFRCEd,SLS,w=0,3mm = 38,5 kNm/m, oproti tomu pro železobeton pouze pro hodnotu MRCEd,SLS,w=0,3mm = 26,1 kNm/m.

Posledním ověřením je posouzení omezení napětí v průřezu od charakteristické MEd,SLS,char = 25 kNm/m a kvazistálé kombinace zatížení MEd,SLS,qp = 18 kNm/m v čase 28 dní. Z tab.1 je zřejmé snížení napětí v betonu i ve výztuži v případě použití vláken v průřezu oproti prvku vyztuženému klasickou výztuží, u kterého navíc nevyhovuje posouzení na napětí v betonářské výztuži od charakteristické kombinace zatížení.
Materiálová nelinearita
Použití vláknobetonu vyztuženého ocelovými drátky je stále častější, a proto je nevyhnutelné simulovat reálné chování tohoto materiálu. Zejména pro beton vyztužený ocelovými vlákny může tato analýza poskytnout výsledky odpovídající skutečnému chování konstrukce oproti lineárnímu výpočtu. Toto chování je velmi ovlivněno tvorbou trhlin, která je typická pro beton obecně. Tažnost vláknobetonu se výrazně zvyšuje díky existenci ocelových vláken až po hodnoty, které jsou velmi blízké chování standardní betonářské výztuže.
Fyzikálně nelineární výpočet představuje velmi silný nástroj pro analýzu jakéhokoliv druhu konstrukce ve stavebním inženýrství, a to nejen z vláknobetonu, ale také z ostatních materiálů. Obecně mohou existovat významné rozdíly výsledků lineárního a nelineárního výpočtu, zejména v případě staticky neurčitých konstrukcí. V rámci lineární analýzy je pro přípravu matice tuhosti zohledněn pouze modul pružnosti materiálu. V tomto případě existuje pouze lineární závislost napětí na základě zvýšení přetvoření. Oproti tomu nelineární výpočet zajišťuje skutečné rozložení napětí a zvýšení únosnosti po dosažení limitního přetvoření, dokud nedojde ke kolapsu založenému na různých hodnotách napětí a přetvoření v závislosti na předem definovaném nelineárním pracovním diagramu
Modifikovaný Mazarsův model poškození
Pro nelineární analýzu byly testovány různé přístupy a materiálové modely [7], kdy se jako nejvýhodnější ukázal tzv. modifikovaný Mazarsův model poškození. Plně fyzikálně nelineární výpočet v rámci metody konečných prvků lze realizovat v programu Scia Engineer především prostřednictvím 2D materiálové nelinearity za použití modifikovaného Mazarsova modelu poškození. Tento původně izotropní model poškození je modifikován do anizotropního tvaru, aby lépe zohledňoval různé chování betonu v tahu a tlaku. Pro potřeby výpočtů zohledňujících také výztuž je dále kombinován s tzv. vrstvičkovým modelem desky. To znamená, že jak beton, tak modelovaná výztuž vstupují do výpočtu automaticky v podobě ekvivalentních vrstev příslušného materiálu, které odpovídají reálné pozici a objemu materiálu v desce. Aplikace tohoto modelu poškození na skutečnou konstrukci byla provedena na rozsáhlém ověřovacím testu základové desky na pilotách v Šanghaji [6].
Základová deska na pilotách (Nanhui projekt v Šanghaji)
Vláknobeton s rozptýlenými ocelovými drátky je velmi často využíván pro základové desky podepřené na pilotách. Také u těchto konstrukcí je velmi podstatné jejich chování z hlediska průhybů. V této studii byly ověřovány hodnoty mezního zatížení konstrukce a deformace právě na drátkobetonové desce podepřené pilotami. Vlastní experiment byl uskutečněn na Tongji univerzitě v Šanghaji v Číně a numerická simulace byla přepočtena firmou Bekaert ve spolupráci se společností Scia [6].
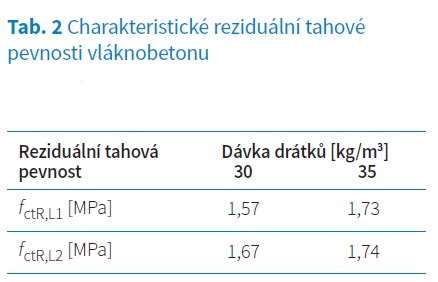
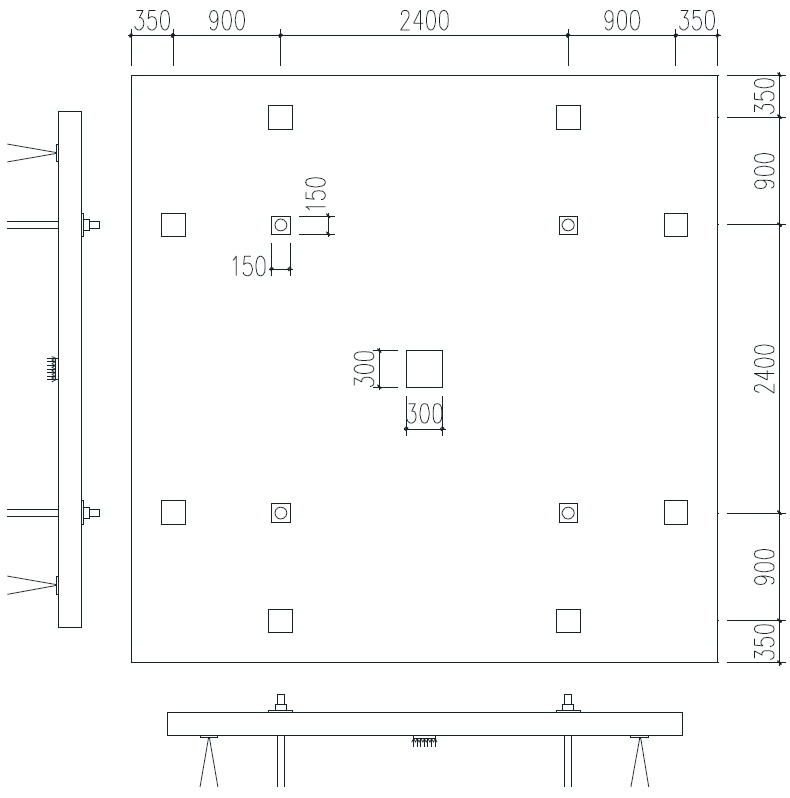
Zatěžovací zkouška byla provedena na betonových deskách C40/50 o rozměrech 4,3 × 4,3 m a tloušťce 187,5 mm podepřené bodovými čtvercovými podporami reprezentujícími piloty. Desky se mezi sebou lišily množstvím ocelových drátků Dramix 5D – 30 kg/m3 a 35 kg/m3. Zatížení bylo vnášeno postupně ve středu desky lisem směrem nahoru. Laboratorními zkouškami na šesti vzorcích byly dle EN 14651 stanoveny materiálové parametry drátkobetonu fR1‑4,m, z nichž byly dopočteny jejich reziduální tahové pevnosti L1, L2, které jsou patrné z tab. 2.
Obě desky byly modelovány plošnými prvky s velikostí sítě 50 mm. S využitím symetrie bylo možné modelovat pouze ¼ konstrukce (2,15 × 2,15 m). Z důvodu výstižnějšího chování po dosažení mezní únosnosti bylo zatížení vnášeno pomocí deformací v místě fiktivní podpory, ze které se následně odečítaly hodnoty reakcí.

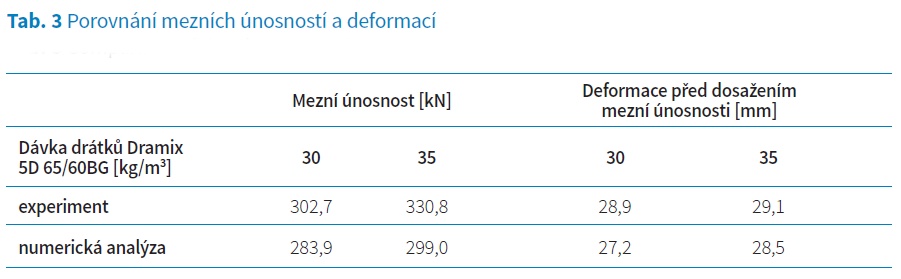
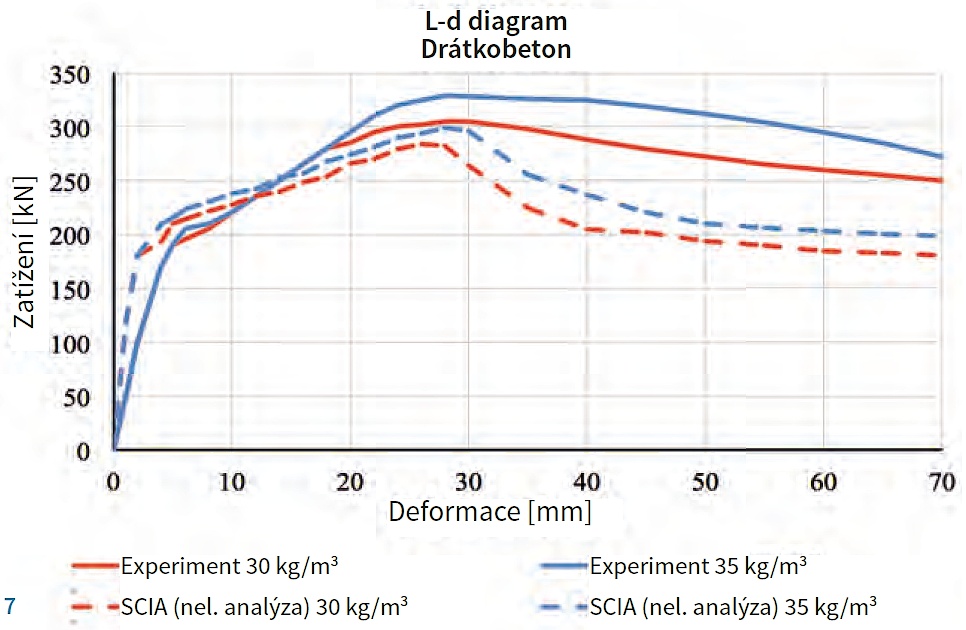
Pro numerickou analýzu byl opět použit již zmíněný Mazarsův model poškození, který ukázal velmi dobrou shodu s experimentem. Mezní únosnost konstrukce byla dosažena při zatížení 283,9 kN (30 kg/m3) a 299 kN (35 kg/m3), kdy mezní tahové přetvoření drátkobetonu dosahuje limitní hodnoty 25 ‰. Porovnání zatěžovacích křivek pro oba typy dávkování drátků je patrné z následujícího grafu.
Typická tahová špička v pracovním diagramu drátkobetonu funguje velice dobře jako lokalizátor trhliny. Toto chování je velmi zřejmé z následujících obr. Červené oblasti znázorňují napětí blízké vzniku trhliny a tato místa se rozšiřují při vzrůstajícím zatížení směrem od středu desky ke krajům. Stále se rozšiřující střední žlutá oblast reprezentuje místa překročení tahové pevnosti, vzniku trhliny a využití reziduální pevnosti drátkobetonu.
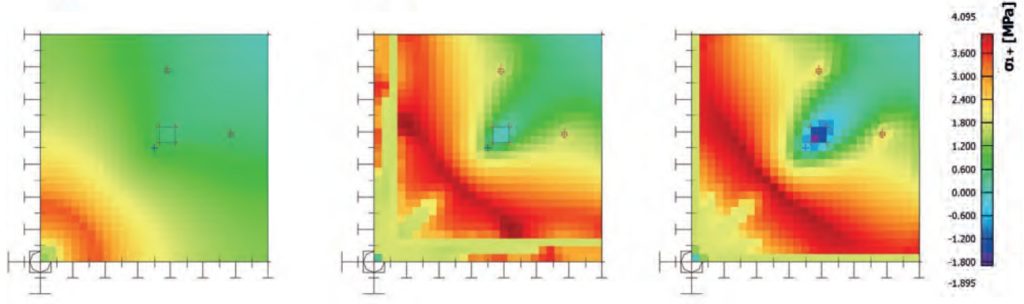
Závěr
Ve spolupráci společnosti Scia s výrobcem ocelových drátků Bekaert bylo vyvinuto unikátní řešení pro návrh a posouzení vláknobetonových desek na základě DAfStb [2] implementované do programu Scia Engineer. Tento nástroj přináší nové možnosti použití pro velmi rychlý, přesný a jednoduchý návrh a posouzení konstrukcí z vláknobetonu vyztuženého ocelovými drátky.
Nelineární metody, vyvinuté za účelem simulace reálného chování konstrukcí, ukázaly velmi dobrou shodu při ověření a porovnání reálných experimentů. V případě Nanhui projektu v Šanghaji byly ověřovány zatěžovací křivky mezního zatížení a deformace u desek z vláknobetonu třídy C40/50 vyztuženého ocelovými drátky Dramix 5D 65/60BG o množství 30 a 35 kg/m3. Srovnání naměřených a vypočtených hodnot ukazuje mírně vyšší hodnoty maximálních zatížení v případě experimentu, což je na straně bezpečné. Deformace odpovídající meznímu zatížení lze však považovat za totožné.
Zdroje
[1] EN 1992 – 1‑1. Eurocode 2: Design of concrete structures – Part 1 – 1: General rules and rules for buildings. European Committee for Standardization (CEN), 2003.
[2] DAfStb Richtlinie. Stahlfaserbeton. Berlin, Germany: German Committee for Structural Concrete (DAfStb), 2012.
[3] Rilem TC 162-TDF. Design of steel fibre reinforced concrete – Method, recommendations, Material and Structures. March 2001.
[4] fib Model Code for Concrete Structures 2010. Lausanne, Switzerland: International Federation for Structural Concrete, 2013.
[5] All-round concrete reinforcement solution. Bekaert.com [online]. © 2019 Bekaert. Dostupné z: www.bekaert.com/en/product-catalog/construction/dramix/all-round-concrete-reinforcement-solution
[6] DLOUHÝ, L., ROLAND, R. Experimental and numerical comparative analysis of a SFRC slab on piles. In: Proceedings of ACI – fib – RILEM Joint Workshop – Fibre Reinforced Concrete: from Design to Structural Applications. Desenzano, Italy, June 27th – 30th, 2018. p. 74.
[7] DLOUHÝ, L., KIKA, O., PAIL, T., VALACH, P. Stanovení průhybů vláknobetonových desek s rozptýlenou výztuží z ocelových drátků s využitím nelineární analýzy. In: Sborník z konference Betonárske dni 2018. Bratislava, 2018.



